Unit 4 Desmos Drawing Project and Function Families
Unit 3 Reflection:
What content/skills have been most interesting to you? The content that has been most interesting to me this year
has been finding the surface area and volume of more complicated shapes. I enjoyed this because it was very interesting
to use something I have done before and modify it.
How have you grown mathematically? I have grown mathematically by broadening my understanding of mathematics
and learning new equations and methods. This has helped me overall grow mathematically and make me better at math
in general.
has been finding the surface area and volume of more complicated shapes. I enjoyed this because it was very interesting
to use something I have done before and modify it.
How have you grown mathematically? I have grown mathematically by broadening my understanding of mathematics
and learning new equations and methods. This has helped me overall grow mathematically and make me better at math
in general.
Unit 2 Reflection: Shadows, Similarity and Right Triangle Trigonometry
1. What has been the work you are most proud of in this unit? The work that I am most proud of this semester would have to be learning trigonometry. I am most proud of this work because I feel like I fully understand trigonometry and all of my work is very good. Since I was able to understand trigonometry so well, I enjoyed it as a whole and learned a very important part of geometry.
2. What skills are you developing in geometry/math? There are a lot of skills I am working on developing in geometry, but some of the main ones are using Google spreadsheets to create graphs, setting up a table to approach mathematical problems, and approaching problems using different methods. I feel like these skills are very important to helping me in the future because they apply to more than just math and can be used in almost any job setting.
3. Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you. Trigonometry is a way of using equations to find missing parts of triangles and other shapes by using the parts you already know. An example would be if you needed to find out the hypotenuse of a triangle, and you had the other sides and one of the angles, you would use the tangent equation so if your other sides were 2 and 3 and your angle was 36 degrees you would do tan(36)=2/3 to find the missing side length.
Problems Of The Week:
1. Problems of the week, or P.O.W.s, have helped me grow mathematically by helping me look at problems from different angles to solve problems that I might struggle with if I had not looked at the problem differently when something confused me or did not seem right. They have also helped me by forcing me to better organize my thoughts in my process of evaluating problems, and later on clearly displaying my work.
2. What skills are you developing in geometry/math? There are a lot of skills I am working on developing in geometry, but some of the main ones are using Google spreadsheets to create graphs, setting up a table to approach mathematical problems, and approaching problems using different methods. I feel like these skills are very important to helping me in the future because they apply to more than just math and can be used in almost any job setting.
3. Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you. Trigonometry is a way of using equations to find missing parts of triangles and other shapes by using the parts you already know. An example would be if you needed to find out the hypotenuse of a triangle, and you had the other sides and one of the angles, you would use the tangent equation so if your other sides were 2 and 3 and your angle was 36 degrees you would do tan(36)=2/3 to find the missing side length.
Problems Of The Week:
1. Problems of the week, or P.O.W.s, have helped me grow mathematically by helping me look at problems from different angles to solve problems that I might struggle with if I had not looked at the problem differently when something confused me or did not seem right. They have also helped me by forcing me to better organize my thoughts in my process of evaluating problems, and later on clearly displaying my work.
S1 P.O.W. #1 Knights
|
S2 P.O.W. #2 Pick-Up Triangles
|
|
1.Yes they can do it.
2.I could only figure out two ways to do it, and the best of these methods took me only 16 moves to flip the knights. Write-up: What we had to do for this P.O.W. was pretty straight forward. We had a 3 by 3 chess board and two black knights on one side, with two white knights on the other side. Our goal was to flip the knights around, so to have the white knights be where the blacks ones were and so forth, in the minimum number of moves. The process I used to figure out how to flip them was pretty simple at first. My original plan was to mirror what I do with one knight and do the same move with the opposing one. This soon led to my knights running out of places to go so I decided to just try to move one group (for example the white knights) to their flipped positions while just moving the other group out of the way when necessary. This proved to be a successful plan to move the pieces but required a lot of moves to complete so I am not sure if it was the minimal amount of moves. The way I kept track of my pieces was by using quarters because I don’t have any chess pieces. I would use heads and tails and to keep the coins separated for tails I would use different states on the back, for example Alabama and New York, and for the heads I used one quarter from the Denver Mint and one from the Pennsylvania Mint. I think that my answer represents the least number of moves because even though I tried all of the different ways I could think of, my only solution I could find took 16 moves or more so therefore I think that 16 moves is the very minimum amount of times it takes to complete this problem. Some other problems that I thought of that are similar to this problem are using pawns instead of knights but with the ability to reverse also. The pawns would maintain their ability to move straight forward for their first move but after that can only go diagonal in any direction. I have not tried this problem but if I had to guess I would say it would be extremely difficult to complete because of your extreme lack of moves available to use. I think I learned how to better approach these types of puzzles and how to think of the problem in a more complex way and to “think outside of the box” a little bit more because the answer is not usually right in front of you in the real world and this P.O.W. helped me by testing skills I will actually use outside of school so I enjoyed it. If I had to grade myself I would give myself a 26 out of 30 because I think I explained my thinking very well in my write-up and showed my process clearly, but I could only find two ways to complete this problem and I felt that even my best method still took a high amount of moves to complete this problem at 16 moves. |
Mark Laffaye P.O.W. 2 Write-up Problem: You must make 2 similar triangles. You have 4 rods to help make these triangles, they are 2, 3, 4, and 6 inches long each. You also have as many rods as you will need extra, with lengths between 1 and 20, but only whole numbers. Using these rods, how many similar triangles can you make? Process: Originally, I was completely lost on how to even make a triangle, much less two triangles that are similar. Once I figured all of that out though, I quickly found my first pair of similar triangles. To try to find the rest of the pairs of similar triangles I tried just using guess and check, but I probably shouldn't have because it took up a lot of space and seemed to waste a lot of work time. The only pattern I could find is using multiples of the numbers on my left triangle to see if it worked. This pattern was pretty simple but I could not find very many similar triangles using the numbers 2, 3, 4, and 6. I was able to tell when my triangles were similar by comparing the side lengths on both triangles, and remembering that triangles can only be similar if you can multiply or divide and find the difference between them. If you try to use addition it will become distorted. Solution: I was only able to find two pairs of triangles that completely worked, but if you can have two side lengths be the same in one of your triangles (which I have no idea about) then I would have a couple more. The first one I had had the first triangles side lengths be 4, 6, 8, and the seconds ones be 2, 3, 4. The second one I found was to use the same lower numbers but multiply by 3 instead of 2. The first triangles sides were 2, 3, 4, and the second ones were 6, 9, 12. These are the two that I found that definitely work. New Problem: A new problem I thought of would be to replace triangles with any shape, and give you 6 numbers you have to use instead of just 4, but the thing is you can make any shape you want as long as all of the lines connect. This would probably be a lot harder because you have to really think about what shape you are going to make that would be best and also having more lines that you have to use would probably limit the shapes you can make. Evaluation: I think that this P.O.W. was especially helpful for me to understand pretty obvious things about triangles that I must've missed in elementary school. Now I will clearly understand how to make a triangle that actually works as a triangle. I might change this P.O.W, or maybe all P.O.W. schedules, by just giving us one full day to work on it, plus just maybe a couple minutes at the end of some classes early on in the P.O.W. instead of just having like 30 minutes in class every once in a while so that the P.O.W. is clearer in our minds while we work. I thought this was one of the better P.O.W’s we have done so far, except I feel like I didn’t get as many answers as I should have. I think this P.O.W. was the perfect level of difficulty for our class, but since I didn’t know much about triangles to start with it was pretty hard for me. I would give myself a 21 out of 25 for this P.O.W. |

Snail Trail Project
I created this "Snail Trail" by taking a single point a duplicating it. I then made the points different colors. After changing the colors I turned on trace mode and then just moved a single circle and all of them followed. After I did this, I turned back on my circle and tried dragging the circle to create a picture. In my opinion this looks better as a final method and that is why I chose to display my circle method. This design shows rotational symmetry around the center of my circle, and reflectional over lines that are marked as hidden.
I created this "Snail Trail" by taking a single point a duplicating it. I then made the points different colors. After changing the colors I turned on trace mode and then just moved a single circle and all of them followed. After I did this, I turned back on my circle and tried dragging the circle to create a picture. In my opinion this looks better as a final method and that is why I chose to display my circle method. This design shows rotational symmetry around the center of my circle, and reflectional over lines that are marked as hidden.

Tessellation Project
Title: Rough Seas Tessellation
1. The idea or theme behind my tessellation is an oil tanker traveling through the ocean, with clouds above it and fish below it. I decided to make my tessellation an oil tanker because I wanted to do a vehicle but drawing a car was really hard and drawing a plane was even harder and it would always end up looking bad and could not tessellate. I also chose an oil tanker out of all of the boats in the world because it is a simple design and also I researched oil tankers in 8th grade for a digital arts project!
2. I started with a square and drew a boat inside of it. I then got scissors and cut out my boat. I then got tape and taped my boat to the top of the square I drew my boat on. If you were to look at this square now you would see a cutout where a boat obviously was on the bottom and the boats shape taped onto the top of the square to form one boat on top of the other.
4. In my opinion tessellations are math. This is my opinion because they need math to be even and if they aren't even with the help of math they wouldn't be tessellations. “A regular polygon has 3 or 4 or 5 or more sides and angles, all equal. A regular tessellation means a tessellation made up of congruent regular polygons.” This quote shows how math is required to make a tessellation by having to use polygons and angles. I can see how somebody might consider a tessellation art because of how they are colored and shaped, but without math they wouldn't be tessellations, because you need the math to make sure that your art can tessellate and if you didn't use math it wouldn’t tessellate correctly. To explain more clearly, tessellations are just shapes repeating over and over, which is mathematical symmetry. “If you look at a completed tessellation, you will see the original motif repeats in a pattern. One mathematical idea that can be emphasized through tessellations is symmetry.”
Sources Cited:
"Tessellations." Tessellations. N.p., n.d. Web. 14 Nov. 2014.
"Math.com Wonders of Math." Math.com Wonders of Math. N.p., n.d. Web. 14 Nov. 2014.
"Math Forum: What Is a Tessellation?" Math Forum: What Is a Tessellation? N.p., n.d. Web. 13 Nov. 2014.
Title: Rough Seas Tessellation
1. The idea or theme behind my tessellation is an oil tanker traveling through the ocean, with clouds above it and fish below it. I decided to make my tessellation an oil tanker because I wanted to do a vehicle but drawing a car was really hard and drawing a plane was even harder and it would always end up looking bad and could not tessellate. I also chose an oil tanker out of all of the boats in the world because it is a simple design and also I researched oil tankers in 8th grade for a digital arts project!
2. I started with a square and drew a boat inside of it. I then got scissors and cut out my boat. I then got tape and taped my boat to the top of the square I drew my boat on. If you were to look at this square now you would see a cutout where a boat obviously was on the bottom and the boats shape taped onto the top of the square to form one boat on top of the other.
4. In my opinion tessellations are math. This is my opinion because they need math to be even and if they aren't even with the help of math they wouldn't be tessellations. “A regular polygon has 3 or 4 or 5 or more sides and angles, all equal. A regular tessellation means a tessellation made up of congruent regular polygons.” This quote shows how math is required to make a tessellation by having to use polygons and angles. I can see how somebody might consider a tessellation art because of how they are colored and shaped, but without math they wouldn't be tessellations, because you need the math to make sure that your art can tessellate and if you didn't use math it wouldn’t tessellate correctly. To explain more clearly, tessellations are just shapes repeating over and over, which is mathematical symmetry. “If you look at a completed tessellation, you will see the original motif repeats in a pattern. One mathematical idea that can be emphasized through tessellations is symmetry.”
Sources Cited:
"Tessellations." Tessellations. N.p., n.d. Web. 14 Nov. 2014.
"Math.com Wonders of Math." Math.com Wonders of Math. N.p., n.d. Web. 14 Nov. 2014.
"Math Forum: What Is a Tessellation?" Math Forum: What Is a Tessellation? N.p., n.d. Web. 13 Nov. 2014.
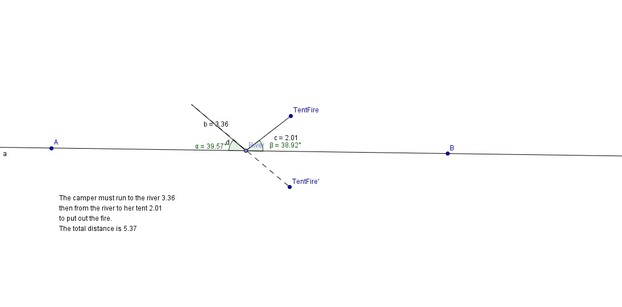
Burning Tent Lab:
1. They appear to be the same.
2. Because the line I made is just a reflection of the line camper to river, as shown by the straight line, It proves that my route is literally the most direct possible using TentFire prime to show this.
3. The point "River" should be on the dotted line of camper to river, to show it is in the middle of the trip.
2. Because the line I made is just a reflection of the line camper to river, as shown by the straight line, It proves that my route is literally the most direct possible using TentFire prime to show this.
3. The point "River" should be on the dotted line of camper to river, to show it is in the middle of the trip.





